科学家也研究魔法吗？看你怎么定义魔法。如果说魔法是我们未曾了解透彻的奇异之事，也许是的。

如果我们站在宏观的经典世界，看待微观的量子世界，就能感受到这种“魔法”气息。比如，处于量子叠加态的那只“死去活来”的薛定谔猫，还有，被爱因斯坦称为“鬼魅的超距作用”的量子纠缠。

甚至，结合信息和计算视角，科学家更近一步提出了量子魔法的概念——那些经典世界无法模拟的量子特性。

这些，都可以纳入量子多体系统的研究视野——大量相互作用的量子粒子组成的物理系统。研究这类问题，需要付出巨大的计算成本，而西湖大学物理系严正团队，致力于发展更高效的模拟计算方法来“严正以待”。

左起：丁一茗（博士生）、严正、王哲（博士后）

2025年严正团队密集发布成果，先后在Nature Communication、PRX Quantum等期刊发表多项重要研究，系统地发展了量子多体系统中纠缠谱、纠缠熵、量子魔法的高效大规模计算方法，并且探究了这些非局域物理量与物态和相变的关系，推动了量子信息学和凝聚态物理的进一步融合。

特别是量子魔法，这是量子信息学中非常前沿的概念，除了用于刻画量子计算的优势度之外，严正团队开始探索量子魔法与量子物态之间是否存在更深层次的联系。与此同时，东京大学的学者也严格证明了严正团队在该研究中涉及到的一类问题。而在2022年，欧洲多国科学家联手提出了一种评估量子魔法的计算公式。多国学者都在聚焦量子魔法，并形成了某种接力。

而本文将从最基本的概念出发，带你感受经典和量子的鸿沟，或许也是对量子魔法的惊鸿一瞥。

扫码收听声音版本，和严正团队聊量子

吸尘器扫过黑色沙发，发出一阵嘶鸣。正当我诧异于这是什么仪式，严正关掉吸尘器，解释说办公室绿植引来不少小虫子，吸掉点儿。于是我们四人坐下，严正教授，王哲博士后，丁一茗博士生。开场抓虫子的行为艺术，无意中暗合了聊天话题。

1940年代，“初代目”电子计算机用灯泡大小的真空管作为基本运算器件，布置在房间里，常引来飞蛾，引发故障。于是，Bug开始表示计算机程序故障或者漏洞，原意是虫子。

无论现在的集成芯片做多小，经典计算机的基本原理没有变过，所有信息都用0和1组成的二进制表示。这种信息的最小单位，被称为比特。又无论经典计算机如何复杂，其底层的经典比特是确定的。真正不确定的，只是那只从现实世界闯入的飞蛾。

作为研究量子体系的学者，严正先聊起了计算机，似乎在引导我从信息视角来重新看待量子问题。而当他说到量子计算机时，我脱口而出：“量子霸权嘛，很有名。”

“现在改了，学界现在说量子加速，”严正打断道，“事情没有那么简单。”

IBM研发的一种量子计算机，采用冷却超导比特的技术路径，温度需降到-272.78℃

在介绍这种转变前，我们先来简单感受下量子力学。可以说，量子力学颠覆了经典的物理学观念。一个量子系统可以处于叠加态，直到被测量时才“坍缩”成其中之一。

甚至更违反直觉的纠缠态。产生纠缠的两个粒子，即便你把他们放在银河系的两端，你观测其中一个，另一个的观测结果会被同时决定。这种“鬼魅的超距作用”，连爱因斯坦都心生怀疑。

如此这般，这般如此，都是量子态的特性。

所幸的是，我们可以用希尔伯特空间、薛定谔方程等数学工具来描述量子力学。数学工具是认知的梯子，但不是认知对象本身。如同物理学家费曼在给本科生上课时的名言——没有人懂量子力学，包括他自己，他出生的的时候不能，他说这话的时候还是不能。但同时，费曼也很敏锐，他是最早提出量子计算机概念的先驱之一。

现在，欢迎来到量子计算的世界，一个用量子比特构建的世界，除了0和1，还有0和1的叠加态。

一个由0和1构成的经典计算机的世界尚且如此复杂，那量子比特所能涌现的特殊到底何在？

然后，科学家尴尬又诚实地发现，许多量子态却仍能被经典计算机通过一种名为Clifford线路的方法高效模拟，包括一些有着很强纠缠的量子态。如同电影《浪浪山小妖怪》里灵山脚下的假雷音寺，一群“经典比特”也可以凭着演技，演一出量子态的好戏给你看。

只是大自然的底层逻辑依然保有自己的神秘，非“经典比特”所能模拟。

学界为此引入了新的概念，把那些依然可以被经典模拟的量子态，称之为稳定子态。进一步，非稳定子性这一概念也被引入，它衡量一个量子态偏离稳定子态的程度，代表的是量子系统中那些难以被经典系统有效模仿的部分，是一种特殊的量子性。这一量度还有一个时髦的别称——量子魔法。

这是从量子计算的视角看问题，但说白了，量子计算机本身就是一个包含大量相互作用粒子的量子多体系统。不过研究量子多体系统所呈现的整体特征，正是严正团队的专业所在，实验室的专业名字就叫量子多体计算实验室。

“这就像是物理学中的社会学，人和人之间涌现出的社会复杂性，才是更迷人的，这和人是由什么物质构成的关系不大。”严正如此比喻。

严正在和团队交流中

当时，博士生丁一茗就跑去和严正讨论，如果一个量子系统的状态能被一个经典系统高效模拟，那么这个系统还足够“量子”吗？换言之，他们开始猜测那些有着量子魔法的量子系统可能相比没有量子魔法的系统更加特殊。

也许，量子魔法也可能刻画一些超越计算科学视角的物理，这是一种交叉视角下重新看待问题。

但问题是，一个量子系统所涌现出来的量子魔法，并不是直接可见的，而是深藏于体系内复杂的作用关系之中。特别是对于量子多体系统，直接研究量子魔法并不容易，计算难度巨大。

一边是一个非常新颖的课题，一边是一个非常年轻的团队。2023年严正从香港大学全职加入西湖大学，丁一茗和王哲几乎是同时加入。丁一茗在复旦读的硕士学位，做的就是量子计算方向。王哲博士毕业于北京师范大学，做的是凝聚态和统计物理。

这个年轻团队试图去探寻关于量子魔法的真经，要离开浪浪山，不管怎么说，一路上千山万水，必须严正以待。

理学院到处是黑板，教授办公室，会议室，走廊的尽头或者拐角，好像是哆啦A梦的任意门，一有灵感就可以随时提笔，然后一头步入黑板背后的世界。

我们的第二次采访约在理学院E4-201会议室，一个两面都是黑板的房间，其中一面书写内容刚刚被擦去，留下层层海浪般的肌理。我在这幅画面前停顿了一下，想到粉笔其实是来一亿多年前白垩纪海洋藻类遗骸沉积而来。

这和量子力学有什么关系？并没有。但是，当这些粉笔写下关于这个世界的数学模型之后，不同模型涌现出来的共通性，才是真正的惊奇。

回到严正团队的工作，他们为量子多体系统建模，并利用计算机模拟来研究他们的性质或者特征。他们把每一个粒子抽象成一个点，并模拟点和点之间到相互作用。但是请注意，量子模型是概率性的，理论上每一种组合状态都有可能出现，只是不同组合状态的概率分布不同。他们有个俏皮的行话，叫作——

Toy Model，玩具模型。

“就好像小孩子玩积木，从最简单的开始搭建，逐渐向复杂逼近。”博士后王哲如此比喻，前半句满是童真，后半句满怀壮烈。

事实上，物理学家从搭建少量格点开始，从最简单的一维开始，逐渐走向复杂。按照目前严正团队所处理的最复杂的问题所构建的可能性，已经逼近了——10的2073次方。

这差不多是同时对25个宇宙的粒子进行排列组合。面对恐怖如斯的计算量，用严正的话来说，就是“算不动，根本算不动。”也许上帝看了都要直摇头。

但是，为什么要硬刚呢？

二战期间，躺在病床上的乌拉姆突然也是这么想的。他是参与曼哈顿计划的专家，卧床的他在玩接龙时获得灵感，和同事冯·诺伊曼一起提出了蒙特卡洛方法，这是一种用大量的随机性统计来逼近求解答案的思想。蒙特卡洛，是摩洛哥一家赌场的名字，乌拉姆的叔叔经常去，赌场的轮盘象征着随机性。一个著名而简单的例子，是用投针统计的方法不断逼近圆周率π。

位于摩洛哥的蒙特卡洛大赌场

严正正是这个学派，笑称为“卡门”。

当一个体系展开后，过于庞大和复杂时，蒙特卡洛方法有点像是——“人口普查”。即通过随机抽选一部分可能的状态，来进行对整体性质的近似评估， 严正团队的目标，就是开发更好的算法，计算原本认为不可能的体系信息，进而促进我们对物理的理解。

比如纠缠熵，听起来就很纠缠很混乱？

熵——本是描述系统无序程度的热力学概念，往往意味着无序。在量子力学中，纠缠熵用于量化系统各部分间量子纠缠强度，它是量子信息科学与凝聚态物理的交汇处的核心角色之一。然而，我们对二维乃至更高维度系统的纠缠熵进行系统性地扫描仍然很困难。

在严正团队所构建的量子体系中，J用来表示粒子间作用的强度。过去的方法，只能给出单个J情况下的所对应的纠缠熵，如果要观察体系的纠缠熵随着J的变化，那就要一次次算。

有一次，严正找博士后王哲聊，说我们想个办法，别再一次次算了，去研究随着J的变化，寻找纠缠熵的变化规律。王哲当时的第一反应是：

“这怎么可能？”

但王哲回去后，沿着严正给的思路，开始尝试后，发现别有洞天。简言之，在计算纠缠熵之前，我们需要先求得J对应的配分函数Z(J)——你可以简单把配分函数当作一种数学工具，某种程度上也代表着一个体系不同构型的概率权重。过去，对Z(J)的计算是计算的主要难点，而且J代表着体系也在不断变化。

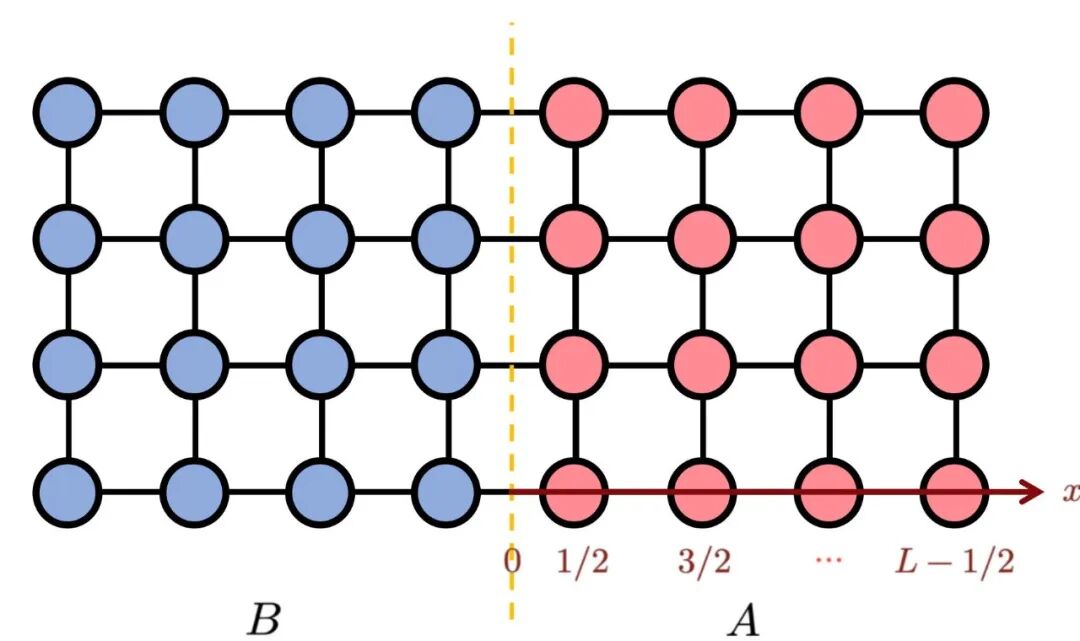
一种二维格点模拟的示意图，目标是研究一个体系内和A和B之间的纠缠强度，体系的尺寸L可以不断扩增，以不断逼近更复杂的情况。J代表体系粒子间作用的强度。

在严正带领下，经过王哲还有丁一茗等同学的持续合作，他们开发出一套方法，突破了这种困局——

随着体系参数J的变化，我们可以这样去定义相邻的J——J0,J1,J2,J3….,Jn，以及它们对应的配分函数Z(Jn)。虽然求配分函数困难，但通过严正团队开发的技巧，他们可以高效求出相临两个配分函数的比值——Z(Jn-1)/ Z(Jn)。然后系统初始的配分函数Z(J0)是已知的，那可以根据比值求出Z(J1)，Z(J2)也可同理求得，依次进行，一连串的配分函数都可以一下子算出来。[Phys. Rev. B 110, 165152 (2024)]，[Nat. Commun. 16, 5880 (2025)]。 （拓展阅读：量子蒙卡新算法，让纠缠熵不再难缠）。

就像一个个多米诺骨牌，依次倒下。严正对此有一个比喻——横扫千军万马。更重要的意义，是终于可以一次看清随着体系参数变化，纠缠熵的变化。

他们还把这个策略，推广到了混合纠缠态的研究中[Phys. Rev. B 111, L241108 (2025)]。也就是量子多体系统里混入了经典不确定性，他们惊奇地发现，在量子临界点上，出现了长程的纠缠结构，也就是粒子可以和远程的粒子发生纠缠，而不是相邻的。临界点也就是体系发生相变的时刻，往往在临界点会有神奇的性质显现。另外，他们还开发了高效计算量子多体纠缠谱的算法，用来刻画量子多体波函数的长程纠缠特征。[Nat. Commun. 16, 2880 (2025)] （拓展阅读：量子多体纠缠计算新范式：抽样约化密度矩阵）。

在这个神奇的点，他们果然看到了神奇，见证量子魔法也许也不远了。

2021年，来自德国、意大利、法国的学者合作提出了评估非稳定子性的一种方法，取名为稳定子雷尼熵。这是为了纪念匈牙利数学家雷尼，是他提出的雷尼熵，对香农信息熵的某种推广。

这个公式的出现，意味着对量子魔法有了一种评估方法。

公式有了，但怎么计算又是另一个问题，原本以为到了“灵山脚下”的严正团队，遭遇了蒙特卡洛里臭名昭著的“符号问题”。一旦遇到“符号问题”，就不能往下做了，这几乎是当时学界共识。当用于采样的权重出现负值或复数值时，概率解释失效，采样误差指数级放大——这就是“符号问题”。

“这是经典方法试图进入到量子世界的时候，遇到的大问题。”丁一茗说。如同来到经典和量子的鸿沟，往下看，是深不见底的未知。

又如同之前的那个比喻，难道千军万马要困在黑暗森林之中？严正团队最终的突破，来自对体系的进一步研究，他们提出了约化泡利算符的概念，巧妙利用体系的对称性，避开了障碍点。

这种解题技巧一般的技术，他们用一个俏皮话比喻——Trick。就是万圣节孩子们说的Trick or treat（不给糖就捣蛋）。Trick可以理解成把戏或者花招。

想要求得魔法，你不得来点花招？

最通俗讲，就是避开走不通的地方，把问题巧妙转化为可以等效计算的模型。当然，之前开发的算法也应用其中，也就是追踪参数J的连续变化所对应的稳定子雷尼熵的变化。

严正团队采用的超算集群之一。由于量子系统的自由度指数发散，尽管发展了高效算法，我们仍需要借助超级计算机来进行研究

这是一个研究的狂喜时刻，如同经历了痛苦迷乱后的突然顿悟，又如同在森林中跋涉，突然获得一双翅膀，飞入天空，望尽天涯路。

严正团队很快用新算法系统地研究了量子魔法在一维和二维量子横场伊辛模型的临界点附近的行为，因为相变点总容易发现奇妙的现象，但是在相变点附近，稳定子雷尼熵的变化似乎看不出太特别的地方。

如果把这个函数描绘成一条曲线，这条曲线在相变点附近，没有特别独特的特征。难道之前所有研究努力都是一场落空？好似取到了无字经书的唐僧，难道要捶胸顿足，然后泪如雨下吗？

大自然又留了一手，内涵就在表象之中。

这条曲线的二阶导数，在相变点附近出现了突变。在相变点附近，二阶导出现了一个尖锐的高峰，而且随着模拟粒子数量的增加，显得越发尖锐，越过相变点，高峰又陡转急下，回归平坦。

量子魔法，居然在相变点也发生了突变，以一种隐藏的数学形式在和物理变化遥相呼应。严正团队发开的算法，也是迄今为止唯一一个可用于研究高维量子多体系统量子魔法和其高阶导数的无偏数值工具。

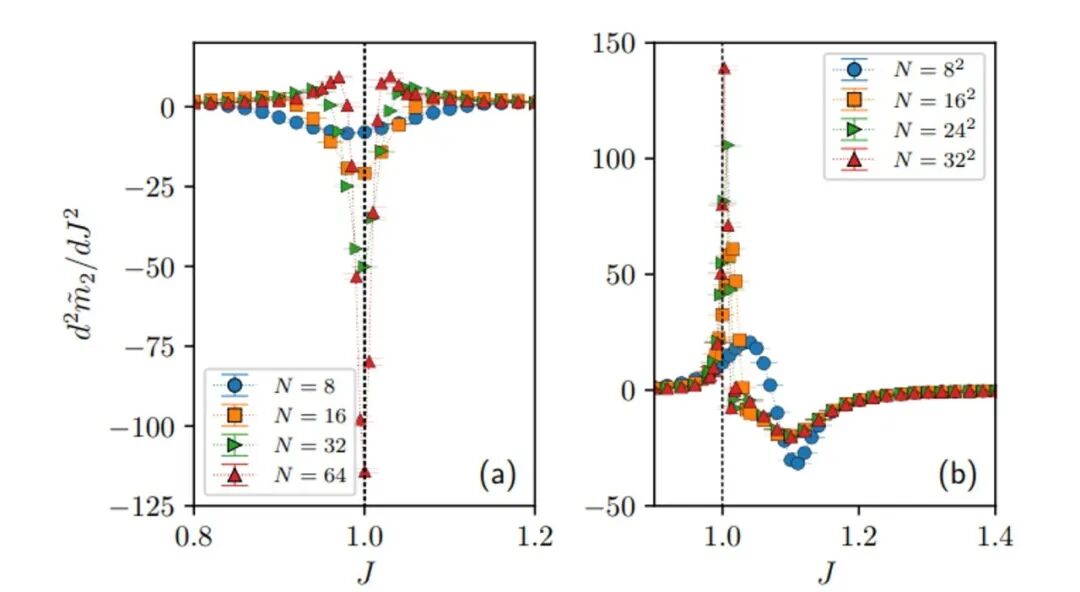
一维（左）和二维（右）量子横场伊辛模型基态的量子魔法（稳定子Rényi熵）关于伊辛相互作用强度高阶导数J的奇异性，这里J=1为量子相变点。不同色彩和符号代表着模拟体系的扩大，随着体系的扩大，尖峰越来越明显。

进一步地，他们还研究了“量子魔法”随系统尺寸扩展的标度行为，或者说随系统模拟的粒子数量扩展后，量子魔法是如何增长的。结果表明，量子魔法整体呈现体积律增长，而其修正项却在量子相变点的两侧展现出截然不同的特征，并在临界点处出现明显的不连续性。

对此，你可以简单理解成一个对应的线性函数，y=ax+b，x代表体系的大小，b就是这个体系的修正项，相变点时b由正转负。就好似修正项是一个提线木偶，在相变点上，它突然消失于舞台，出现在观众席上，穿越于无形。

严正团队提出猜想：这些修正项可能不仅仅是微小的修补，而是携带着更深层次的普适物理信息。[PRX Quantum 6, 030328 (2025)] （拓展阅读：物理学中真有“魔法”，它代表一类量子资源）。

仅在严正团队的工作公布两个月后，东京大学的 Masahiro Hoshino 等人从共形场论角度出发，在解析上严格证明了体积律修正项的普适性。特别地，对于一维量子系统，这些修正项与边界共形场论中的一些理论密切相关，成为通向量子临界行为和共形场论一扇新的窗口。共形场论主要研究的就是在临界点，体系表现出的共性不变形，比如缩放、旋转等操作都不会改变体系的性质。

又是一处巧合，计算机模拟和理论证明重逢了。

云谷校区的“太空梭”

最后一场采访在学术环进行，聊到尾声，我看了一眼学术环外的太空梭，恰似论文图表上二阶导数的尖峰。对于一个世界的穿行者来说，从表象出发，穿越理性意义上的抽象，发现无论是黑白上由格点构建的模型、还是经典计算机里的0和1，以及我们依然无法全然认知的量子世界，依然有路相通相连。

又如费曼所言——What I cannot create, I do not understand——制造一个东西的前提，是充分理解它，如果你制造不出来，说明还没有理解透彻。量子计算机也许同样，又也许，我们对量子魔法的探索也才刚刚开始。

而回首科学的历程，何尝不是把一个个魔法，消散为日常的过程？

论文地址 https://doi.org/10.1103/pyzr-jmvw

致谢 Acknowledgment 

上述工作得到国家高层次青年人才项目、国家博士后面上项目、以及西湖大学专项经费等项目的支持，并得到来自西湖大学高性能计算中心的计算支持。

主要论文 

[1] Evaluating Many-Body Stabilizer Rényi Entropy by Sampling Reduced Pauli Strings: Singularities, Volume Law, and Nonlocal Magic,Yi-Ming Ding, Zhe Wang, Zheng Yan,PRX Quantum 6, 030328 (2025)

[2] Bipartite reweight-annealing algorithm of quantum Monte Carlo to extract large-scale data of entanglement entropy and its derivative, Zhe Wang, Zhiyan Wang, Yi-Ming Ding, Bin-Bin Mao & Zheng Yan, Nat. Commun. 16, 5880 (2025)

[3] Tracking the variation of entanglement Rényi negativity: A quantum Monte Carlo study,Yi-Ming Ding, Yin Tang, Zhe Wang, Zhiyan Wang, Bin-Bin Mao, Zheng Yan,Phys. Rev. B 111, L241108 (2025)

[4] Sampling reduced density matrix to extract fine levels of entanglement spectrum and restore entanglement Hamiltonian,Bin-Bin Mao, Yi-Ming Ding, Zhe Wang, Shijie Hu, Zheng Yan,Nat. Commun. 16, 2880 (2025)

[5] Measuring the boundary gapless state and criticality via disorder operator,Zenan Liu, Rui-Zhen Huang, Yan-Cheng Wang, Zheng Yan, Dao-Xin Yao,Phys. Rev. Lett. 132, 206502 (2024)

严正实验室介绍

量子多体计算课题组主要开展量子多体理论和数值计算方向的研究，以及与之相关的量子模拟/计算、量子材料交叉学科研究，比如——

1)量子阻挫磁性: 自旋液体、新奇物相、临界行为等；

2)量子模拟，冷原子阵列，量子绝热计算等；

3)受限多体系统和晶格规范场，如量子dimer/loop模型等；

4)量子多体纠缠，如纠缠熵、纠缠谱的行为；

5)发展新的量子多体算法；

除了上述方向之外，课题组也乐意积极拓展量子多体相关的交叉学科。

实验室主页 

www.westlake.edu.cn/faculty/zheng-yan.html

电子邮箱：

zhengyan@westlake.edu.cn

每年招收1-2名博士生，同时欢迎申请本组博士后！