时间：2023年9月16日-2023年9月17日 9:00-17:30

Time：9:00-17:30, September 16, 2023 - September 17, 2023

地点：西湖大学云谷校区E4号楼233教室

Venue: Room 233, Building E4, Yungu Campus, Westlake University

组织者: 西湖大学理学院 赵永强博士

Organizer: Dr. Yongqiang Zhao, PI of School of Science, Westlake University

日程/Schedule:

1、主讲嘉宾/Speaker：Prof. Weidong Gao, Center for Applied Mathematics, Tianjin University

主讲题目/Title：Zero-sum problems in Abelian groups

摘要/Abstract: Let G be a finite abelian group written additively and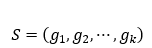be a sequence of elements from G (repetition allowed). We call S a zero-sum sequence if 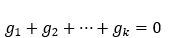(the identity element of G). Zero-sum theory in Abelian groups is to study the conditions that ensure the existence of a zero-sum subsequence of prescribed properties. Zero-sum theory has attracted a lot of attention and developed rapidly in the past thirty years. We will present some results and open problems in this direction.

2、主讲嘉宾/Speaker：Prof. Daguang Chen, Tsinghua University

主讲题目/Title：Symmetrization and Eigenvalue estimates for the Laplacian in Riemannian manifolds

摘要/Abstract: In this talk, we will report the symmetrization technique in Riemannian manifolds and submanifold. As applications, we obtain the estimates of the eigenvalues and eigenfunctions of the Laplacian with Dirichlet and Robin boundary conditions. This is partly joint work with Prof. Haizhong Li and Dr. Yilun Wei.

3、主讲嘉宾/Speaker：Prof. Erxiao Wang, Zhejiang Normal University

主讲题目/Title：密铺镶嵌领域的完整分类研究

摘要/Abstract: 密铺或镶嵌是一种基本数学结构，广泛出现在自然和科技领域，如蜂窝、晶体、分子结构 、纳米材料等。报告人与香港科技大学严民等经过六年合作攻关，以共约两百页的四篇文章(arXiv: 1804.03770, 1805.07217, 1903.02712, 1907.08776)研究了用全等五边形“边对边”密铺球面的完整分类；其中三篇论文经过两年多审稿后发表: Tilings of the sphere by congruent pentagons I, II, III. Adv. Math., 394 (2022).

    他们建立了顶点分布统计、多种剖分构造、多种组合和几何引理、相邻角推导符号系统、用代数几何求解高阶三角函数方程组等一整套理论方法。近两年他们又各自独立带领学生团队（硕士生廖艺熹、本科生徐应允、钱品任等）完全分类了球面四边形单密铺，运用了分圆域和三角丢番图方程的新方法：Tilings of the sphere by congruent quadrilaterals I, II, III. arXiv: 2110.10087, 2205.14936, 2206.15342.

    从而彻底解决球面边对边单密铺的百年难题。

    由十余名本硕博组成的浙师大密铺镶嵌创新工作室正在报告人带领下分组探索着错边、曲边、多密铺等各种曲面上的密铺的完整分类问题，及其在3D密铺的应用（比如单密铺空间的四面体完整分类这个有着2300多年历史的公开难题），已取得了不少工作积累。

    报告人也将综述这个本来小众的领域在近几年的多个突破（Viazovska; Yang-Zong; Mann-Mann-von Derau; Rao; Kedlaya-Kolpakov-Poonen-Rubinstein; Greenfeld-Tao; Zhang; Smith-Myers-Kaplan-Strauss等），探讨其与生物、材料和人工智能等领域的交叉。听众无需具备数学背景，欢迎所有师生参加。

4、主讲嘉宾/Speaker：Prof. Changhao Chen, Anhui University

主讲题目/Title：Sum-product theorems and applications

摘要/Abstract:  I will show proofs for sum-product estimates over real numbers and finite fields respectively, and show an application on estimating of exponential sums. I will also talk about the discretized sum-prodcut estimates, and its applications on fractal geometry.

The talk are mainly based on (1) Been Green, Sum-product phenomena in F_p: an brief introduction; (2) Bourgain, The discretized sum-product and projection theorems.

讲座联系人/Contact:

理学院 王老师  wangqiuhui@westlake.edu.cn